【資料結構】圖形結構(Graph)基礎篇(2) - 擴張樹(Spanning Tree)

✨擴張樹(Spanning Tree)
擴張樹(Spanning Tree)又稱花費樹,一個圖形的擴張樹是以最少的邊來連結圖形中所有的頂點(且須避免循環)。
- 一棵包含圖上所有頂點的樹,稱作該圖的擴張樹。
- 一張圖的擴張樹可能會有很多種。
- 完全連通圖才有擴張樹 (不連通時,則稱為擴張森林)。
- 擴張樹的權重為樹上每條邊的權重總和。
假設今天有n個頂點的無向圖形擴張樹,則會有n-1個邊。
使用BFS方式追蹤產生的擴張樹稱為寬度優先擴張樹;使用DFS追蹤產生的擴張樹則稱為深度優先擴張樹。
✨花費最少擴張樹(Minimum Spanning Tree)
一副連通加權無向圖中擁有最小成本(權重)的擴張樹就稱為花費最少擴張樹。
那麼為何需要找到花費最少擴張樹?
因為很多情境都可由圖形來表示,例如從台北到西班牙轉機的距離就可以以此找出花費最少的方法。
找出一個加權圖形中花費最少擴張樹可以利用以下三種演算法(當然不止這三種):
- Kruskal's Algorithm
- Prim's Algorithm
- Sollin's Algorithm
這三種演算法皆是greedy algorithm(貪婪法則)。
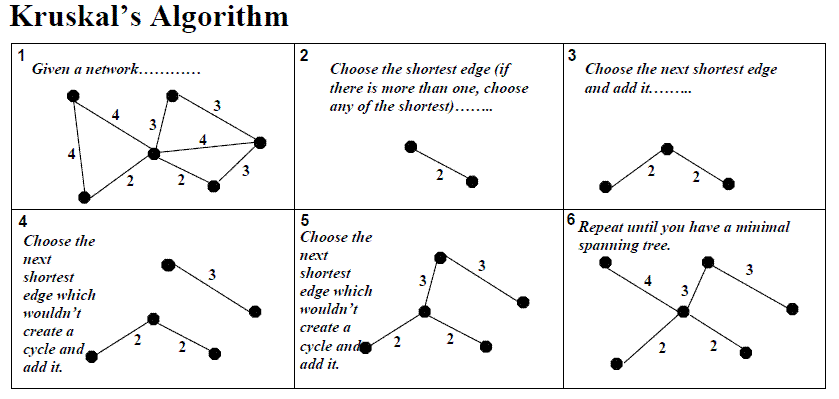
🌸Kruskal's Algorithm
這個演算法較容易實作,由Spanning tree中花費最少的邊出發,每一次都選擇目前尚未被選擇的最少花費的邊,且避免形成循環,直到邊的個數為n-1(頂點為n)即找出花費最少擴張樹。

🌸Prim's Algorithm
先從Spanning tree中找一個頂點V作為起始點,找出與V相連且還沒有被選取的頂點裡面加權值最小的邊,直到找到n-1個邊(頂點為n)。


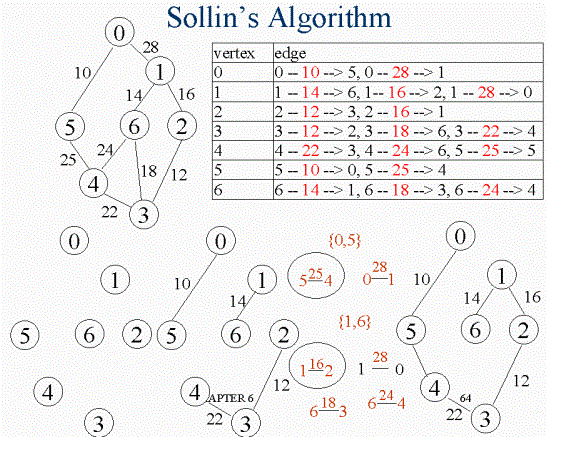
🌸Sollin's Algorithm
每次選擇花費最少的子圖,並且再選取花費較少的邊將這些子圖相連(不能造成循環),直到邊數為n-1(頂點為n)停止。