【資料結構】平衡搜索樹 - 紅黑樹、B樹(2-3,2-3-4樹)、B+樹

2-3樹與2-3-4樹為B樹的特例，所以特別拿出來細講。
今天主要講解的內容包括：2-3樹、2-3-4樹、紅黑樹、B樹、B+樹。

何謂「平衡搜索樹」？

平衡搜索樹常見的有：AVL、紅黑樹、B樹(2-3與2-3-4樹都是B樹的特例)

平衡樹的定義：若非空樹，則必須滿足父節點的左子樹與右子樹高度差絕對值不大於1。
這其中，AVL、紅黑樹皆屬於平衡二元搜索樹。

※平衡搜索樹（Balanced Search Tree）新增、刪除及搜索的時間複雜度皆為O(logn)
不同平衡搜索樹的高度(height)：

AVL樹：高度≦logn
紅黑樹：高度≦2logn
2-3樹：高度≦logn
2-3-4樹：高度≦logn

專業術語

節點(node)：用以代表資料(data)、狀態(state)。
樹根(root)：樹中最上層的節點，也是唯一一個父節點為null的節點。
子(Child)節點：一個節點的下一層節點。
子樹(subtree)：去掉根節點，其餘的節點可分割成任意個數互斥的集合，每一個集合也都符合樹的定義。
葉節點(leaf)：沒有child/subtree的節點。
分支(degree)：一個node擁有的子樹個樹。
階度(level)：以根節點的階度為1，其餘節點的階度為其父節點的階度+1。
高度(height)：此樹的最高階度。
siblings：擁有相同父節點的節點們，為兄弟節點。

常見到有人說這是3階,4階的樹，這裡的3階指的是一個節點最多可以擁有三個子節點，4階則是指一個節點最多可以擁有四個子節點。

2-3樹

為何會叫2-3樹？原因為每個節點可以有2或3個子節點。

滿足二元搜索樹的基本性質—左小右大，但不是二元樹(因為最多可以擁有三個子節點)。
節點可以放1或2個元素(1個元素時有2個孩子；2個元素時有3個孩子)
是一棵絕對平衡的樹(左右子樹高度一定相同，所有葉節點皆在同一level)

當今天有2個元素(b,c)3個子節點時，左子節點≦b ; b<中子節點≦c ; c<右子節點
如下圖所示

2-3樹的元素新增

假設今天有一筆資料{53,23,77,45,11,2,44,77,93,26,32,16,87,11}
按照搜索樹的性質依序加入資料，下方為新增的步驟

當輸入到77時，一個節點有3個元素，此時需要進行平衡。

將53(大小位於中間的元素)往上提變成根節點，左子節點為23，右子節點為77。

接著輸入45,11，當輸入到11時左子樹又有三個元素，因此需要再平衡。

將23往上提，11與45分別拆成左、中子節點。

接著輸入2,44,77。

再輸入93時，右子樹的元素為3個，需要再次平衡，將77往上提，如此一來根節點變成3個元素，因此將53再往上提一層，左子樹為23右子樹為77。

接著輸入26，一樣需要平衡。

輸入32。

輸入16，進行平衡。

最後輸入87,11無須平衡，完成。

2-3樹的元素刪除

刪除的部分稍微麻煩一點，需要判斷刪除的元素位置，以剛剛我們建好的2-3樹為例：

假設今天要刪除93，不影響任何節點，直接刪除即可。
假設今天要刪除16，而16是11的右子節點，這個子節點中只有一個元素，則須將父節點的左子樹最大值拿來替補父節點，再用父節點替補刪除的節點16，如下圖所示。
假設今天要刪除44，44非葉節點，底下還有左子樹與右子樹，我們需要將左子樹的最大值來做替補。
假設今天我們要刪除根節點的23，那就顯得非常麻煩了，首先需要將根節點左子樹最大值11替補23，再將左子樹的11與其子節點11合併，最後將中子樹32與左子樹合併。
假設今天要刪除77(由根節點開始搜索，第一個碰到的77)，先將左子節點77替補父節點77，再將77與子節點87合併，再將根節點53替補為77與87的父節點，將左子樹的32替補為根節點，完成。

2-3-4樹

為何會叫2-3-4樹？原因與2-3樹相同，只不過2-3-4樹的每個節點可以有2、3或4個子節點。

當一個節點有1個元素，則會有2個子節點，
當一個節點有2個元素，則會有3個子節點，
當一個節點有3個元素，則會有4個子節點。

與2-3樹的性質基本相同，可以參考2-3樹的介紹。

2-3-4樹的元素新增

假設今天有一筆資料{23,66,34,12,1,77,34,23,44,77,1}

加入資料23,66,34。

再加入12時，根節點的元素變為4個，需要進行平衡，將中節點23往上提成根節點，12變為左子樹，右子樹為34與66。

加入1,77。

加入34後右子節點的元素變為4個，需要再次平衡，將中節點34往上提，左邊的34與右邊的66,77變為根節點的中、右子樹。

加入23,44。

加入77後需要再次平衡。

輸入1之後左子節點變為4個元素，需要將中間元素1往上提，但此時根節點也變為4個元素，再次將根節點的中間元素23往上提，左子節點為1，右子節點為34,66。

2-3-4樹的元素刪除

拿上方建好的2-3-4樹作為例子。

刪除葉節點的12，毫無影響直接刪除即可。
刪除非葉節點的1，將其左子節點的1提上來替補，再將1與23合併，最後將根節點23替補為左子樹，將右子樹最小值替補根節點進行平衡。
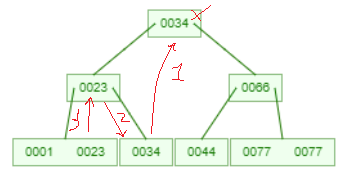
刪除根節點34，先將左子樹底下的最大值替補根節點，再將左子樹23替補34，最後將左子節點最大值替補父節點23。(請忽略敘述，直接看圖理解。)

红黑樹(Red–black tree)

根據《算法導論》中紅黑樹必滿足以下五種特性：

每個節點要不是紅色的，不然就是黑色的。
根節點一定是黑色的。
樹葉節點(最後的空節點)一定是黑的。
如果一個節點是紅色，那他的子節點都是黑的。
從任意一個節點到葉子節點，經過的黑色節點數是一樣的。

保持黑平衡(從根節點到葉子節點所經過的黑色節點數一樣)的二元樹，嚴格來說不是平衡二元樹。

2-3-4樹轉換成红黑樹

一個2-3-4樹可以轉換成不止一種型態的紅黑樹，但一個紅黑樹僅能轉換成一種2-3-4樹。

假設根節點僅有一個元素，則將之設為紅黑樹的根節點；
若根節點有一個以上的元素，則隨意取一個設為紅黑樹的根節點，要注意的是，同個節點拆分出來的元素是紅色的。

這是取自nullzx的圖

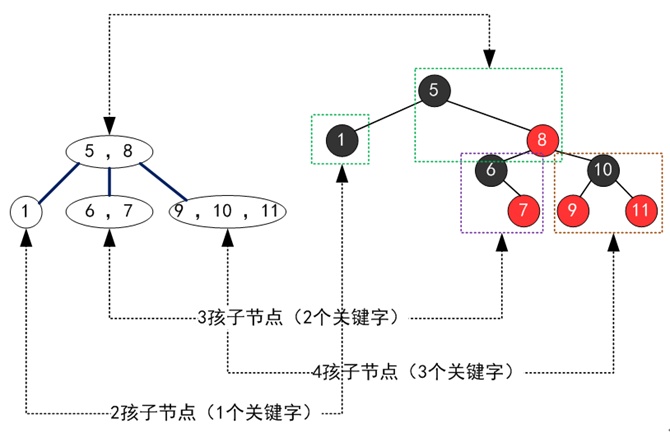
大致了解一下即可，只要了解二元搜索樹及紅黑樹的性質就可以輕鬆轉換。

雖然紅黑樹和AVL樹的時間複雜度都為O(logn)，但是紅黑樹的高度(2logn)比AVL樹(logn)高，所以在紅黑樹上「查找」較AVL樹慢，儘管如此，紅黑樹卻比AVL樹重要且常用，原因為紅黑樹添加與刪除元素的速度較AVL樹快。若光只查詢，AVL樹查詢的速度快於紅黑樹；若需要頻繁的新增與刪除元素，紅黑樹則優於AVL樹。