【資料結構】圖形結構(Graph)基礎篇(1)
起源為瑞士的數學家尤拉解決Koenigsberg bridge problem(七橋問題)。
圖形結構提供了簡單的方式來描述一個問題、系統或狀況等。
與樹狀結構的差異為,樹狀結構是描述節點與節點之間的層次關係。
📜定義與種類
一個圖形是由頂點集合V與邊集合E所組成,數學上通常用G = (V,E)表示。
圖形結構具有以下特徵:
- 基本上是由頂點(Vertices)與邊(Edges)兩個部分所構成。
- 有方向性稱為有向圖(Directed Graph)、無方向性稱為無向圖(Undirected Graph)。
- 圖形的特點之一為資料也可以儲存在個別邊上。邊上的資料可以表示從這個邊的一個頂點至另一個頂點的花費(cost)。這種成本存在邊上的圖形稱為「網路」。
下方為示意圖:
依據線段(Edge)有沒有方向性可分為無向圖及有向圖:
-
無向圖(Undirected graph)
邊集合中的每一個邊都沒有方向性。 -
有向圖(Directed graph)
邊集合中的每一個編都有方向性,以指向下一個頂點。
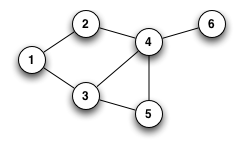
此無向圖G1的點集合與邊集合為:

V(G1)={1,2,3,4,5,6}
E(G1)={(1,2), (1,3),(2,4),(3,4),(3,5),(4,5),(4,6)}
此有向圖G2的點集合與邊集合為:
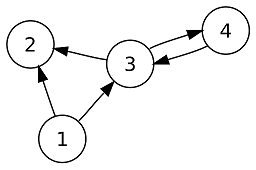
V(G2)={1,2,3,4}
E(G2)={(1,2), (1,3),(3,2),(3,4),(4,3)}
樹也是一種圖,但是樹可以出現環、連通,而樹不行。
注意,圖形不能有自我迴圈(self-loop)。
💬圖形結構的用詞
圖(1)

圖(2)
- 頂點(Vertex):也可稱為資料節點(Node),例如圖(1)的1,2,3,4。
- 邊(Edge):每個頂點的連線就稱為邊。
- 相鄰(Adjacent):例如圖(2)的1,2相鄰。
- 路徑(Path):某個頂點到某個頂點的過程。
- 連通(Connected):在一"無向圖"中,任何成對頂點之間皆有路徑存在。
-
強連通(Strongly connected):
在"有向圖"中,任何成對頂點之間皆有路徑可以相互到達對方。
-
弱連通(Weakly connected):
在"有向圖"中,至少有兩個頂點無法以有向路徑相互到達對方。
-
簡單路徑(Simple path):路徑上除了起點和終點可以相同之外,其餘頂點均不相同。

-
循環(Cycle):若有一條簡單路徑的起點頂點與終點頂點相同,則稱這條路徑為cycle。
-
分支度(Degree):(無向圖)為連接至該頂點的邊之個數。比如圖(2),1的分支度為"2",4的分支度為"4"。
有向圖還會區分為外分支度(Outdegree)與內分支度(Indegree)。 -
子圖(Subgraph):圖中的某一部分。
-
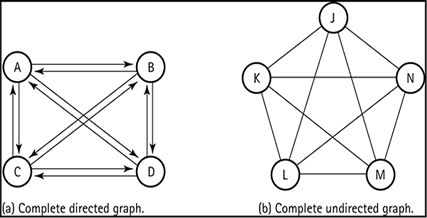
完整圖(Complete Graph):是一個擁有最多非重複邊線的圖:
- 無向圖:若圖具有n個頂點,則具有最多的非重複邊個數達
n(n-1)/2時,此圖稱為完整圖。 - 有向圖:若圖具有n個頂點,則具有最多的非重複邊個數達
n(n-1)時,此圖稱為完整圖。
🔎表示方式
常用的表示方式:相鄰矩陣(Adjacency Matrix)、相鄰串列(Adjacency List)
🎈相鄰矩陣(Adjacency Matrix)
對無向圖而言,根據項點數n,宣告一個n×n的二維矩陣。
矩陣中,每個1就代表該兩個項點有連線。
- 無向圖的相鄰矩陣必為對稱(Symmetric),對角線皆為0,因為自己與自己本身無法相連(
A[1][1]、A[2][2]....A[i][j])其儲存空間為n(n-1)/2。 - 有向圖的相鄰矩陣不一定為對稱,但當有向圖為完整圖時也會是對稱矩陣。
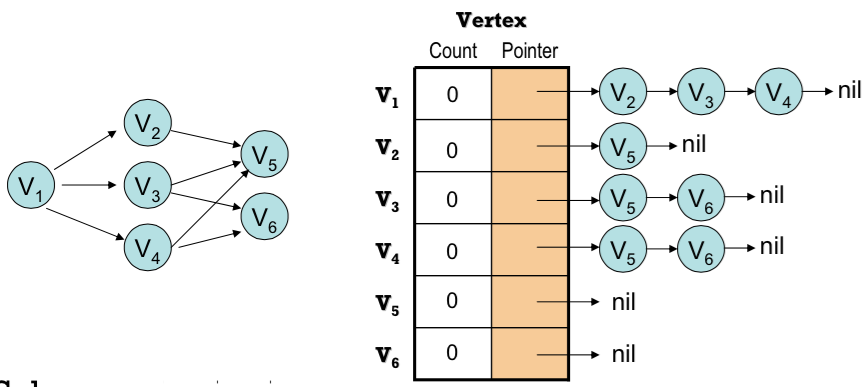
🎈相鄰串列(Adjacency List)
有幾個頂點(n)就需要幾條相鄰串列與一個大小為n的一維陣列,其中A[i] 所存放的是頂點i 的相鄰串列,此串列中毎個Node皆記録著與頂點i 相鄰之其它頂點。
-
無向

-
有向

📍圖形追蹤(Traverse Graph)
圖形中的所有頂點都被拜訪到,且僅被拜訪到一次。
分為DFS深先搜尋與BFS廣先搜尋。
📌深先搜尋(Depth First Search)
包含遞迴應用的概念,因此可利用堆疊(Stack)保存走訪過程中間所走過的點。
如同前序追蹤,先遇到的頂點就先探索,如果節點有子節點,首先對其進行探索。
除非另有說明,否則通常從左到右。
如果從任何已走訪過的頂點,都無法再走訪到一個尚未被走過的頂點時,則結束走訪。
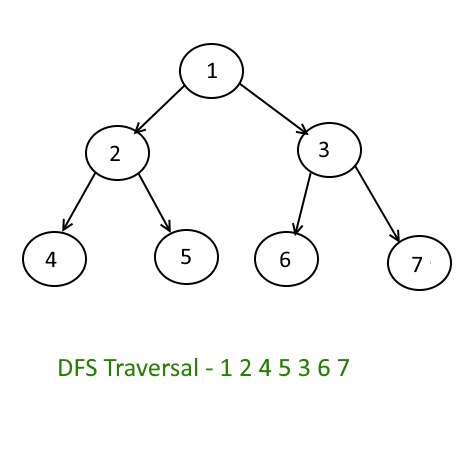
PS.DFS之順序並不唯一除非規定“拜訪時,依Node編號由小到大拜訪”才會唯一。
我們可以利用DFS進行**拓撲排序(Topological Sort)**也可找到有向圖中的Strongly Connected Component(SCC)。
📌廣先搜尋(Breadth First Search)
BFS是廣義的層級探索(Level-Order Traversal),將之從樹推廣至圖。
BFS運作流程基本上與DFS差不多,但BFS是利用佇列(Queue)保存走訪過程中間所走過的點。
由起始頂點15 開始走訪。
所有相鄰至15且尚未被拜訪過的頂點,都會在下個步驟裡一一被走訪。
而相鄰至這些被走訪頂點且尚未走過的頂點,又將被一一走訪;重複上述,直到無頂點可被拜訪為止。

🔸AOV Networks與Toplogical
AOV全稱Activity On Vertex,假設G = <V, E>為一個"有向圖",其中頂點表示工作(Activity),線段表示工作執行之先後次序關係。
應用: 求合理的工作執行順序,即:拓樸順序(Topological Order)
🔸拓樸順序(Topological Order)
- 找出一個無前導(內分支度為0)的頂點將此頂點輸出。
- 刪除此點及其線段。
- 直到所有頂點已輸出,或剩下的點皆有前導存在。

- 若AOV Network有cycle,則無Topological Order。(
∵無法決定誰先做) - 不具cycle的AOV Network,其Topological Order ≥1組。(
不一定唯一)
🔹AOE Networks
AOE全稱Activity On Edge,在有加權的有向圖上以Edge表示工作(Activity),Vertex表示事件(Event),Edge上具有加權值,表示工作完成所需的時間。與AOV不同之處在於,AOV以Vertex表示工作,而AOE是以Edge表示工作。

完成此計畫所需之最少(最起碼)的工作時數?
求從Start → End事件之最長路徑長度即:求Critical path (臨界路徑)的長度。
上圖有可能的路徑為
- 0→1→4→5→6 (持續時間=15)
- 0→1→2→5→6 (持續時間=16)
- 0→2→5→6 (持續時間=13)
- 0→2→3→5→6 (持續時間=20)
- 0→3→5→6 (持續時間=17)
最長路徑的長度為20,因此有一條路徑為Critical path(臨界路徑)。
由於在AOE Networks中有些活動可以並列地進行,所以完成工程的最短時間是從開始點到完成點的最長路徑的長度(路徑上各活動持續時間之和)。路徑長度最長的路徑叫做關鍵路徑。
最早開始/最脕開始時間
在AOE網路上所有的活動皆有的時間,最晚開始時間指一活動在不影響整個計畫完成之下,最晚能夠開始進行的時間。

以上圖計算最早及最晚時間,結果如下: